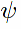 as shown below. Proposition
2.2 in the paper states that
as shown below. Proposition
2.2 in the paper states that
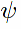 is independent of the
variables s and t. The computational proof of this
result using Maxima is explained in detail below. The actual Maxima
commands are shown in blue color.
is independent of the
variables s and t. The computational proof of this
result using Maxima is explained in detail below. The actual Maxima
commands are shown in blue color.
Supplement to
"Positive linear functionals without representing measures"
Eq. 2.6 in the paper defines
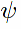 as shown below. Proposition
2.2 in the paper states that
as shown below. Proposition
2.2 in the paper states that
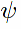 is independent of the
variables s and t. The computational proof of this
result using Maxima is explained in detail below. The actual Maxima
commands are shown in blue color.
is independent of the
variables s and t. The computational proof of this
result using Maxima is explained in detail below. The actual Maxima
commands are shown in blue color.
We start from the matrices J and W:

and
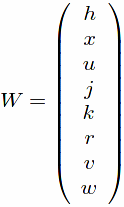
Following the notation in the paper, we write
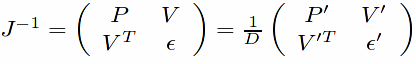 .
.
Here
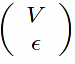 form the last column of
form the last column of
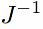 , and D is the
determinant of
, and D is the
determinant of
 that we factor out from
that we factor out from
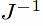 . Then,
. Then,
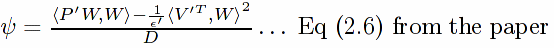
Proposition 2.2 in the paper claims that
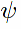 is independent of
is independent of
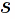 and
and
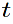 .
.
Let
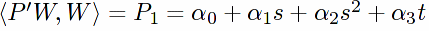
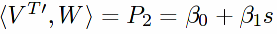
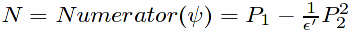

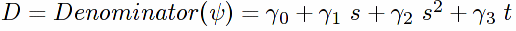
N and D above will enable us to form Eq. (2.7) in the paper:
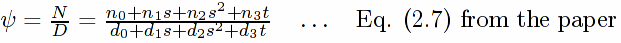
where:
 ;
;
 ;
;
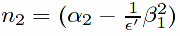 ;
;
 ;
;
 ;
;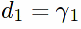 ;
;
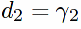 ;
;
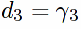
Then:
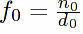 ,
,
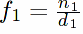 ,
,
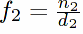 ,
,
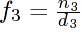
and our goal is to show that
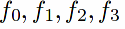 are all equal by showing that
are all equal by showing that

For easy reference we repeat the
representations of
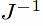 and
and
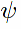 :
:
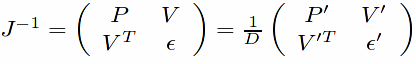
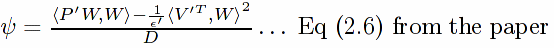
The table below shows the correspondence between the symbols used in the paper and the Maxima variables we use:
|
Symbol from paper |
Variable name used in Maxima program |
|
|
inv |
|
|
D |
|
|
rho_p |
|
|
rhopW |
|
|
rhopWW |
|
|
epsilon_p |
|
|
V_p |
|
|
VpW |
/** Beginning of Maxima commands. All Maxima commands are in blue. **/
/** Turn on timing of calculations - each calculation is then timed for cpu time and elapsed time. **/
showtime:true$
/** define matrices J and W **/
J: matrix([1, a, b, c, e, d, f, gg, x], [a, c, e, b, f, gg, d, h, j], [b, e, d, f, gg, x, h, j, k], [c, b, f, e, d, h, gg, x, u], [e, f, gg, d, h, j, x, u, v], [d, gg, x, h, j, k, u, v, w], [f, d, h, gg, x, u, j, k, r], [gg, h, j, x, u, v, k, r, s], [x, j, k, u, v, w, r, s, t] );
W:transpose([h,x,u,j,k,r,v,w])$
/** The next 3 commands allow factoring out the determinant of J from J-1 .
detout environment variable allows the determinant to be factored out from the inverse, and it needs the doallmxops and doscmxops to be set to false.
**/
doallmxops: false$
doscmxops: false$
detout: true$
/** numInv is the Adjoint of J, and D is the determinant of J. ***/
inv:invert(J)$
numInv:num(inv)$
D:denom(inv)$
/** reset the matrix computation parameters **/
doallmxops: true$
doscmxops: true$
/** compute the components that go in to
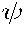 , equation (2.7) **/
, equation (2.7) **/
rho_p:submatrix(9,numInv,9)$
rhopW:rho_p.W$
rhopWW:rhopW.W$
epsilon_p:numInv[9,9]$
V_p:submatrix(9,col(numInv,9))$
VpW:transpose(V_p).W$
/** isolate s, s^2, t coefficients as well as terms independent of s and t in rhopWW .
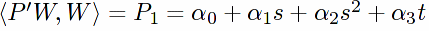
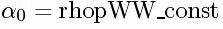
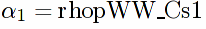
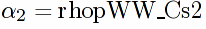
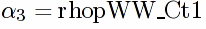
**/
rhopWW_Cs1:ratcoef(rhopWW, s, 1)$
rhopWW_Cs2:ratcoef(rhopWW, s, 2)$
rhopWW_Ct1:ratcoef(rhopWW, t, 1)$
rhopWW_const:expand(rhopWW-rhopWW_Cs1*s-rhopWW_Cs2*s^2 rhopWW_Ct1 * t)$
/** isolate s, s^2, t coefficients as well as terms independent of s and t in D:
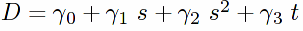

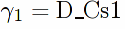
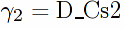
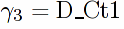
**/
D_Ct1:ratcoef(D,t,1)$
D_Cs1:ratcoef(D,s,1)$
D_Cs2:ratcoef(D,s,2)$
D_const:expand(D-D_Cs1*s-D_Cs2*s*s-D_Ct1*t)$
/** VpW has an s1 term, and terms independent of s and t. Isolate these.
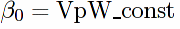
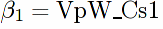
**/
VpW_Cs1:ratcoef(VpW,s,1)$
VpW_const:expand(VpW-VpW_Cs1*s)$
/** epsilon_p is independent of s and t. We redefine epsilon_p as ep for convenience **/
ep:epsilon_p$
/** compose the terms f0, f1, f2, f3 for equation (2.9)
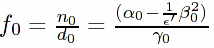
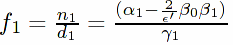
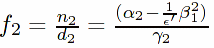

**/
f0:(rhopWW_const-(1/ep)*(VpW_const)^2)/D_const$
f1:(rhopWW_Cs1-(2/ep)*(VpW_const*VpW_Cs1))/D_Cs1$
f2:(rhopWW_Cs2-(1/ep)*(VpW_Cs1*VpW_Cs1))/D_Cs2$
f3:rhopWW_Ct1/D_Ct1$
/** you can store these values in their non-simplified form to disk so that you do not have to recalculate them again. This is particularly true for f0, which is time and space intensive to simplify. To save f0 to disk, for example, do the next command.
Note: "save" saves the expression in maxima lisp format, which you can readily load back into maxima with the "loadfile" command. However, if you want a readable text output, you need to use the "stringout" command on the expression.
**/
save("/home/easwaran/L/2009/f0.maxima", f0)$
/**Simplify f1, f2, f3.
Warning: Trying to simplify f0 will hang unless you do as described below. **/
ratsimped_f1:ratsimp(f1)$
ratsimped_f2:ratsimp(f2)$
ratsimped_f3:ratsimp(f3)$
/** save these simplified expressions **/
save("/home/easwaran/L/2009/ratsimpedf1.maxima", ratsimped_f1)$
save("/home/easwaran/L/2009/ratsimpedf2.maxima", ratsimped_f2)$
save("/home/easwaran/L/2009/ratsimpedf3.maxima", ratsimped_f3)$
/** The next step is the most time-consuming one. It will not work unless your Lisp Engine is allowed to use large temporary heap space, and your maxima temporary directory has large enough storage. Here is how we proceeded:
1. Recompile SBCL, as explained in the SBCL web page
http://sbcl.sourceforge.net/getting.html under the heading "Installing from source". When you configure your make environment, you can specify
"--dynamic-space-size 25600" to allow the Lisp engine to use up to 25GB of temporary heap space. Install the re-compiled SBCL following instructions in the same web URL mentioned above, under the section "Installing from Binary".
2. By default Maxima uses your home directory (on Unix systems) as its temporary working directory. You can re-set it by the Maxima command:
maxima_tempdir="/path/to/new/tempdir"
where the quoted path is a directory on a file system with large enough space, and where the user has read/write permissions.
After recompiling SBCL and installing it, start Maxima again, adjust the maxima_tempdir if necessary, and then read from disk the stored value of f0, and simplify it.
**/
loadfile("/home/easwaran/L/2009/f0.maxima")$
ratsimped_f0:ratsimp(f0)$
/** After f0 is simplified, you can load back simplified versions of f1, f2 and f3, and check f0/f3, f1/f3, f2/f3. These will all be equal to 1 as claimed in the paper **/
loadfile("/home/easwaran/L/2009/f1.maxima")$
loadfile("/home/easwaran/L/2009/f2.maxima")$
loadfile("/home/easwaran/L/2009/f3.maxima")$
/** These are all 1, completing the proof of Proposition 2.2 **/
ratsimp(f0/f3);
ratsimp(f1/f3);
ratsimp(f2/f3);
Here is a link to the actual expression f0=f1=f2=f3.
Here is a sample maxima session output.
This is the directory listing showing the sizes, in bytes, of the numerator and denominator of J^(-1), as well as the raw and simplified expressions f0, f1, f2, f3.
PDF version of this file.
HTML version of this file.